Chi ha studiato come informatico, o si sente tale, sa bene cosa sono gli AND, OR e NOT, che tutto gira attorno a 0 e 1. Ma sono concetti che, i vari livelli di astrazione introdotti dai sistemi operativi prima e dai virtualizzatori e container dopo, restano lontani dalle attività quotidiane.
Peró siamo nei pressi di una rivoluzione epocale, avviata con i computer quantici, che spiazzerà molti di noi. Per essere protagonisti in questa rivoluzione si dovrà tornare a capire le basi del nuovo mondo, ma per capirne le basi si dovranno avere solide le basi del vecchio.
Questa riflessione l’ho fatta nel cercare di rispondere ad una domanda che mi è stata posta: un qbit a quanti bit corrisponde? La risposta è: per rappresentare n bit servono n qbit, ma per rappresentare n qbit può servire un numero infinito (o enorme) di bit. È un concetto semplice da enunciare, ma difficile da capire, si rischia di farne un dogma.
Quindi, prima di avventurarmi in disparate spiegazioni, ho pensato di rivedere le basi e mettere nero su bianco in questo articolo alcuni concetti del vecchio mondo relativi ai circuiti booleani. Giusto per porre le basi e dare un riferimento a chi vuole avventurarsi nel nuovo mondo. Infatti per lo studio dei computer quantici i circuiti booleani sono di gran lunga il modello più semplice per fare delle generalizzazioni in quanto sono il modello più vicino alla realtà fisica dei computer.
Ma attenzione daró per assodati i concetti ed i formalismi dell’ algebra booleana. Non riparto del tutto da zero.
Tutti sanno che qualsiasi elaborazione si voglia fare é possibile con dei circuiti di tipo OR, AND e NOT. Questi circuiti sono dell porte logiche nel senso che applicano ai valori di ingresso le funzioni relative per fornire un risultato in uscita. In inglese, e nel resto del testo, queste porte vengono chiamate gate (cancelli).
Notiamo che tutte hanno 2 valori di ingresso ed 1 di uscita, tranne il NOT.
Definizione 1 Qualsiasi funzione Booleana f : {0, 1}n → {0, 1}m è calcolabile tramite un circuito Booleano C usando solo gate di tipo AND, OR, e NOT. Per questo tali gate sono considerati universali.
Ma é interessante (ed utile) analizzare come tale circuito C potrebbe non essere univoco. Quindi il problema che si pone é quello di trovare un circuito C il piú efficiente possibile, dove per efficiente si intende un circuito il più piccolo possibile. Piccolo non per le dimensioni ma per il numero ed il tipo di gate che utilizza. Infatti tale numero influenza direttamente il tempo impiegato per il calcolo della funzione nella macchina di Touring (il modello generico di macchina ad operazioni sequenziali alla base dei computer attuali).
Consideriamo un circuito per realizzare la funzione XOR
![]()
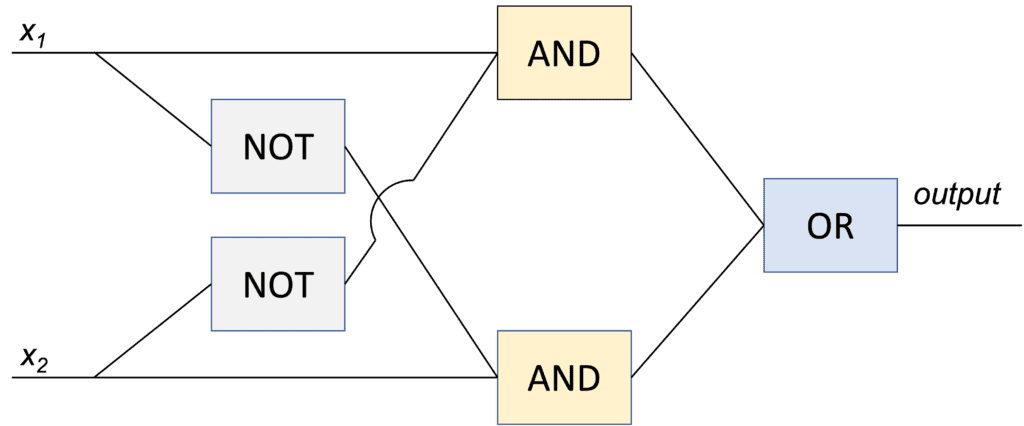
Ovviamente è realizzato con gate universali, ma è immediato fare altre due osservazioni:
Nella realtà deve esistere un meccanismo che permetta una tale suddivisione del dato di input e conviene renderlo esplicito nei modelli dei circuiti. Quindi si considera un nuovo tipo di gate chiamato DUPE (duplicate) che ha come input un bit e come output fornisce due copie identiche dell’input.
Con questa precisazione il circuito diventa:
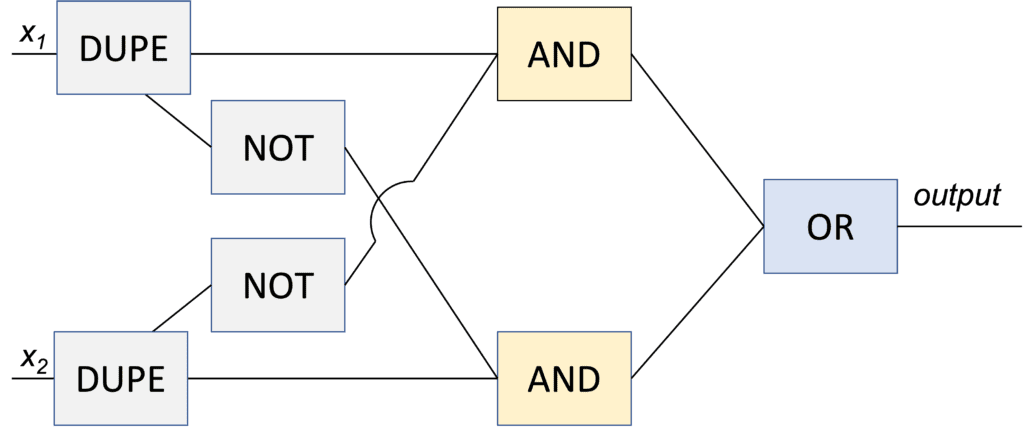
Dopo queste considerazioni si rivede la precedente definizione, per cui:
Definizione 1a I gates universali sono quelli di tipo AND, OR, NOT e DUPE.
In realtà si può ridurre questo insieme di gates perché sia AND, OR e NOT possono essere tutti sostituiti con dei NAND. Rcordiamo che: ![]() Con la regola di De Morgan possiamo sostituire gli OR con NAND e NOT:
Con la regola di De Morgan possiamo sostituire gli OR con NAND e NOT:
![]()
Poi si possono eliminare gli AND poiché: ![]() Quindi l’OR diventa:
Quindi l’OR diventa: ![]() Siamo arrivati a poter utilizzare sologate di tipo NAND e NOT per realizzare qualsiasi circuito. Se consideriamo l’uso del NAND nel modo seguente:
Siamo arrivati a poter utilizzare sologate di tipo NAND e NOT per realizzare qualsiasi circuito. Se consideriamo l’uso del NAND nel modo seguente: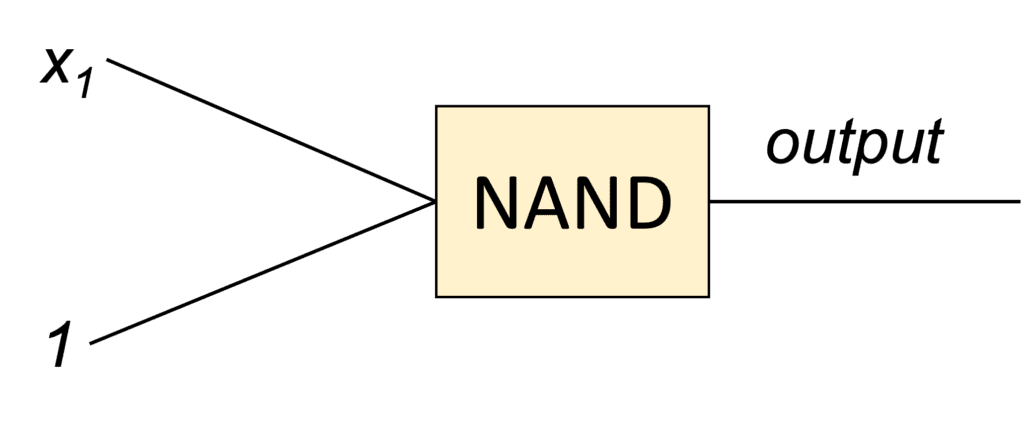 si vede come, forzando ad 1 uno dei due ingressi del NAND possiamo simulare un gate NOT. La particolarità è nel ingresso forzato ad 1 che viene chiamato ancilla bit, ossia un bit costante che facilita la realizzazione di un obiettivo specifico.
si vede come, forzando ad 1 uno dei due ingressi del NAND possiamo simulare un gate NOT. La particolarità è nel ingresso forzato ad 1 che viene chiamato ancilla bit, ossia un bit costante che facilita la realizzazione di un obiettivo specifico.
a questo punto possiamo rivedere la Definizione 1a:
Definizione 1b I gates universali sono quelli di tipo NAND, e DUPE utilizzando gli ancilla bit.
Possiamo vedere che qualsiasi circuito C può essere convertito in un circuito C’ che realizza la stessa funzione e questa conversione può essere effettuata in modo efficiente riducendo il tipo di gate necessari. Da un punto di vista pratico nella realizzazione dei processori, significa che possiamo vederli come un insieme di gate tutti uguali che, connessi in modo differente possono realizzare tutte le funzionalità necessarie. Ciò è possibile perché, come abbiamo visto, esiste un gate universale con cui possiamo realizzare qualsiasi cosa.
Rimane in sospeso un aspetto che pochi prendono in considerazione. Le operazioni effettuate da questi circuiti sono quasi sempre irreversibili. Ossia dato un input di segnali x1, x2, … xn il circuito calcola un output y, ma dato il valore y di tale output non è possibile risalire ai vari xi che lo hasnno prodotto. In pratica solo il NOT è un gate che permette questo.
Ma della reversibilità computazionale ne parleremo in un altro articolo.